PHYSICS - Forces 02
OPENING QUESTION: A box is accelerating down a ramp
None Today!
How would we use Newton's 2nd Law to analyze that situation?What insights would Newton's 1st Law offer as we analyzed that situation?Now let's say that same box is sliding down a ramp at a *constant* rate? How would Newton's 1st help us there?
WORDS O' THE DAY:
- Force ("Push" or "Pull")
- Newton (kgm/s2)
- Newton's 1st Law ("An object will continue whatever it is currently doing unless acted on by an unbalanced force")
- Newton's 3rd Law
- (Short Version: "Forces ALWAYS come in pairs")
- (Quick memory aid version: Noun1 Verb Noun2, Noun2 Verb Noun1)
- (Formal Version: For every force acting on one object, there is an equal and opposite force acting on a second object)
- Force Diagram (A sketch showing ALL forces acting on an object)
- Net Force Diagram (A sketch showing only the resulting (net) forces acting on an object)
FORMULAE OBJECTUS:
- F = ma (Newton's 2nd Law)
═══════════════════════════
WORK O' THE DAY
Nuts and bolts of forces: A NEWTON is a measure of force. As such, a NEWTON is also a vector (magnitude and direction).
Let's practice some vector math:
We'll keep in mind that all forces will be in the x or y planes as indicated. Positive values will be up (in y) and right (in x) and negative values will indicate motion to the left (in x) and down (in y)
To wit:
1) You pull on your kid brother's arm with a force of 3.0 N to the right and your cousin pulls on your kid brothers legs with a downward force of 4.0 N.
Sketch the situation
Do a Newton's 1st analysis of the situation and write your response in a well-crafted sentence (or two)
Calculate the MAGNITUDE of the resulting vector
Calculate the resulting ANGLE to the horizontal at which the resulting force occurs.
Show those values on your sketch
- My video solution is HERE (Ack, it looks like I said 5.3 degrees (should be 53 degrees)
═══════════════════════════
2) You pull on your kid brother's arm with a force of 3.0 N to the right and your cousin pulls on your kid brothers legs with a downward force of 4.0 N another cousin jumps in and pulls on your kid brothers other arm with a force 10. N to the left..
- Sketch a force diagram for the situation
- Now please sketch a NET force diagram for the situation
Do a Newton's 1st analysis of the situation and write your response in a well-crafted sentence (or two)
Calculate the MAGNITUDE of the resulting vector
Calculate the resulting ANGLE to the horizontal at which the resulting force occurs.
Show those values on your sketch
My written solution is HERE
═══════════════════════════
3) Your on a tug-o' war team engaged in an *epic* struggle against another team. Each team is located on each side of a nasty steaming pit of mud (and who knows what else
).
Each team is connected to the other team by a nice, thick rope.
Your team has 5 individuals each pulling in the same direction with 105 N of force each. The other team also has 5 individuals who each pull in the exact opposite direction with 85 N of force each. Which team exerts the most force?
Write a force diagram that accurately depicts this situation
Now please do a NET FORCE diagram to accurately show this situation
Do a Newton's 3rd analysis of the situation and show how each team is actually generating the force on the rope and include a written response (this one will be a wee bit nasty!) Hint: Would this competition be possible if she side were wearing roller skates on a frozen pond?
Mushing on... Now please do a Newton's 1st analysis of the situation and write your response in a well-crafted sentence (or two)
Calculate the MAGNITUDE of the resulting vector
Now make sure to include the correct *direction* of the net force
Let's further say that the members of your team each have a mass of 101 kg and the members of the *other* team have a mass of 102 kg each. Use Newton's 2nd to do an analysis of HOW MUCH (that is what Newton's 2n specializes in after all!) the OTHER team is accelerated towards the steaming pit of
My solution is HERE
═══════════════════════════
4) The following forces are acting on an object with mass of 98.5 kg:
F1 pulls to the left with 33 N of force
F2 also pulls to the left with 88 N of force
F3 pulls to the right with 101 N of force
F4 pulls up with a force of 99 N of force
F5 pulls down with a force of 201 N
Notice that this is a fairly abstract/generic problem so we don't worry about gravity or the ground or any such since nothing like that is mentioned.
Sketch a force diagram
Now sketch a NET force diagram
Now please calculate the magnitude of the resulting vector
Now please calculate the ANGLE that vector makes to the horizontal
5) A 1.75 kg mass is hanging from a rope attached to the ceiling of a classroom as shown
Sketch a force diagram
The problem lacks *what* additional information to allow us to do any sort of analysis?
Now let us say this object is at rest, how does that help us?
How much force is the object pulling on the rope?
How much force is the rope pulling on the object?
═══════════════════════════
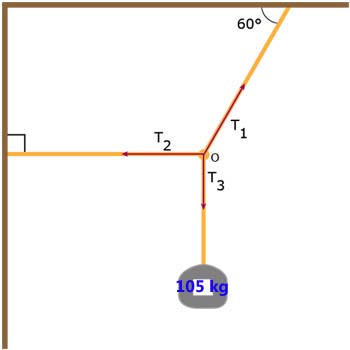
6) Now let's evaluate the object supported by a horizontal rope and a vertical rope hanging at rest as shown below. (Let's make that 60. degrees to add another sig fig)
What are the weasel words here? What do they allow us to do?
How much force does the weight of the mass exert downwards?
Notice that the rope T1 is pulling upwards at an angle of 60. degrees. Further, notice that rope T2 is supporting no vertical forces whatsoever. That means that we must find the vertical component of rope T1 and that MUST equal T3. Why?
Do that now
Notice that the horizontal component of force of T1 MUST equal T2 (why?)
Calculate those now.
My written solution is HERE
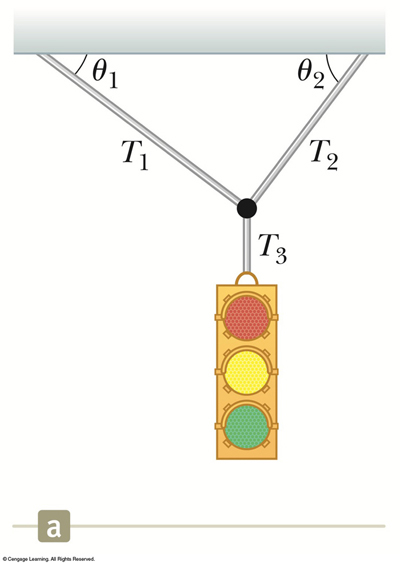
7) A stoplight is suspended by cables as shown below and is at rest:
7a) Junior Varsity Standard Version (This is a tough but a wee more gentle than b & c below):
Consider the stoplight with mass of 75 kg hanging at rest as shown above. Angle 1 is 37.0 degrees and angle 2 is 53.0 degrees. The mass of the stoplight is 75.0 kg. Find the forces T1 and T3 if we know that T2 = 590 N
- Sketch a force diagram
- Use the Alternate Interior Angle theorem to find helpful angles
- Use the weight of the stoplight to find T3
- Show the component (horizontal & vertical) forces for T1 and T2
- Write an equation that shows the horizontal components = 0
- Use those to solve for T1
My written solution is HERE
7b) Varsity Version (This is a tough one):
Consider the stoplight with mass of 75 kg hanging at rest as shown above. Angle 1 is 37 degrees and angle 2 is 53 degrees. The mass of the stoplight is 75 kg. Find the forces T1 , T2 , T3 (pretend you DON'T know T2 )
- Sketch a force diagram
- Use the weight of the stoplight to find T3
- Show the component (horizontal & vertical) forces for T1 and T2
- Write an equation that shows the horizontal components = 0
- Use those to solve for T1 in terms of T2 (Note: this won't be an answer quite yet. It's just like algebra where you have two equations with two unknowns and you're trying to solve one of the unknowns. Remember that?)
- Write an equation that shows the vertical components = 0
- Substitute the value you found for T1 in terms of T2 above. Substitute your value for T3 above so now you have one equation with one unknown (*whew*)
- How will you find T2
My written solution is HERE & HERE
7c) Advanced Varsity Version (This is *REALLY tough*)
Imagine we don't have ANY numeric values at all. No force values, no angles.
*gulp*
When I was a student I kept wanting/needing/pleading with my instructors to NOT give me problems without numbers... it seemed really weird to do problems in the abstract.
What I didn't know was how important to my learning of physics it was to process a problem and THEN worry about the numbers.
Towards that end I'm going to have you do just a wee bit of processing practice now. Remember, I will ALWAYS ask you to work a difficult problem for as long as you can work productively. This is another example of the Goldilocks Principle: Don't work too long on this problem, don't give up too soon.
Do a Newton's 1st analysis of the situation (Hint: the object is at rest, that means the stoplight isn't accelerating which means the forces acting on it MUST be balanced. That means the horizontal forces must be balanced AND the vertical forces acting on the stoplight MUST be balanced to
Derive an equation for each of the component (vertical and horizontal) forces for T1 and T2 (hint: Dig back into the dim dark days of geometry and recall the alternate interior angle formula!)
- Solution Hint #1 is HERE
- Next Steps Hint/Solution is HERE
- Last Steps Hint/Solution is HERE
WOW!